Firstly, let’s see actual pi to a decent level of precision: 3.1415926535897932384626433
Can Revit handle high precision pi calculations?
As a test, let’s use a circle with a diameter of 2000mm (radius of 1m). Using the above precision, the area should be equal to pi in m².
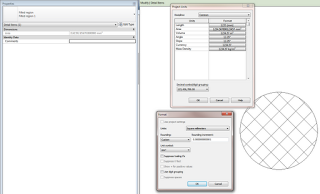
Make a new project in Revit, no template, Metric. Draw a Filled Region with radius of 1000mm. The Properties Palette reports the area as:
3.142m²
Ok, obviously we need to increase the precision of Area in our Revit project. Into:
Manage – Project Units – Area.
Set Units to square millimetres, Rounding – Custom, Rounding increment: 0.000000000001 (I couldn’t get Revit to accept any higher – it would just say ‘Invalid Input’, which I take to mean “what you’re asking for is a bit ridiculous”.)
Properties box for the filled region NOW reports: 3141592.854703690900 mm² 3141592.653589793238 (same amount of digits from the definition of pi)
The percentage of inaccuracy between the two? 0.0000000640165425247805 % (the Revit value is slightly larger)
This was a value difference of 0.201113897662 mm²
However, I am prepared to accept the above level of precision, at least in 99.999994% of my projects 🙂
The lesson? If you are going to use Filled Regions for areas AND you want good precision, make sure you adjust your Project Units accordingly.
And in 99.999994% of cases, I'd absolutely agree. In this case however, my inner pedant kicked in 😉
The filled region example in the post was just the easiest way to demonstrate the point. What I was actually trying to do was with volume calculations and schedules and was a bit more complex. Even bringing rounding into the equation wasn't taking out the error and giving me the answer I wanted. I guess I was just surprised that what to me is quite a simple calculation to me should be that inaccurate.
Just don't forget that pi exist in Revit as a function : PI()
http://revitez.blogspot.fr/2010/10/pi-existe-alfredo-la-rencontre.html
And in 99.999994% of cases, I'd absolutely agree. In this case however, my inner pedant kicked in 😉
The filled region example in the post was just the easiest way to demonstrate the point. What I was actually trying to do was with volume calculations and schedules and was a bit more complex. Even bringing rounding into the equation wasn't taking out the error and giving me the answer I wanted. I guess I was just surprised that what to me is quite a simple calculation to me should be that inaccurate.